retroposa.blogg.se

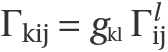
Note that for a sphere, the metric tensor is defined as g = Matrix(,]).

(I have pasted my source code here : Riemann, find_metric). Supplying this g to the code results in the flat_metric. In 3-dimensions for coordinates (r, theta, phi), this translates to g = Matrix(,]). The metric tensor is given as flat_g = Matrix(,]). The curve element is defined as following : flat_metric = r**2*sin(theta)**2*TensorProduct(dphi, dphi) + r**2*TensorProduct(dtheta, dtheta) I am having some issues with determining the Christoffel symbols for a flat sphere (r = constant, theta, phi). Using SymPy.Diffgeom library, I am trying to determine the Christoffel symbols for a given metric tensor.